Las funciones trigonométricas son las funciones cuyo argumento, o variable independiente, es un ángulo. Estas usualmente incluyen términos que describen la medición de ángulos y triángulos, tal como seno, coseno, tangente, cotangente, secante y cosecante.
Los ángulos en las funciones trigonométricas se expresan como radianes. Los radianes son otra manera de medir la apertura de un ángulo, así como lo son los grados, que están en función del radio de una circunferencia.
Definición de las funciones trigonométricas en el triángulo rectángulo
Un triángulo rectángulo es un polígono de tres lados, con un ángulo recto (igual a 90º). Los lados que delimitan el ángulo recto se llaman catetos, y el lado opuesto de mayor longitud es la hipotenusa.
Las funciones o razones trigonométricas son las relaciones entre los catetos y la hipotenusa en un triángulo rectángulo con respecto a uno de los ángulos agudos. Tenemos entonces que para cualquier ángulo agudo del triángulo rectángulo:
- el seno del ángulo (se abrevia sen) es la razón o la división de la longitud del cateto opuesto (CO) entre la longitud de la hipotenusa (H);
- el coseno del ángulo (se abrevia cos) es la razón entre la longitud del cateto adyacente (CA) entre la longitud de la hipotenusa (H),
- la tangente del ángulo (se abrevia tan) es la razón entre la longitud del CO entre el CA, esto es igual a la división del seno entre el coseno,
- la cotangente del ángulo (se abrevia cot) es la razón entre el CA y el CO,
- la secante del ángulo (se abrevia sec) es la razón entre la hipotenusa y el CA, y
- la cosecante del ángulo (se abrevia csc) es la razón entre la hipotenusa y el CO.
Por ejemplo, para el triángulo rectángulo en la imagen, tenemos las siguientes razones trigonométricas:
| Ángulo α | Ángulo β | |
|---|---|---|
| Cateto opuesto (CO) | b | a |
| Cateto adyacente (CA) | a | b |
| Hipotenusa (H) | c | c |
| Seno | CO/H=b/c | CO/H=a/c |
| Coseno | CA/H=a/c | CA/H=b/c |
| Tangente | CO/CA=b/a | CO/CA=a/b |
| Cotangente | CA/CO=a/b | CA/CO=b/a |
| Secante | H/CA=c/a | H/CA=c/b |
| Cosecante | H/CO=c/b | H/CO=c/a |
Ejemplo
Dado un triángulo rectángulo cuyos catetos miden 3 y 4 cm y la hipotenusa mide 5 cm, las funciones trigonométricas de cada ángulo agudo serán:
| Ángulo α | Ángulo β | |
|---|---|---|
| Cateto opuesto (CO) | 3 cm | 4 cm |
| Cateto adyacente (CA) | 4 cm | 3 cm |
| Hipotenusa (H) | 5 cm | 5 cm |
|
Seno |
CO/H=3/5 | CO/H=4/5 |
| Coseno | CA/H=4/5 | CA/H=3/5 |
| Tangente | CO/CA=3/4 | CO/CA=4/3 |
| Cotangente | CA/CO=4/3 | CA/CO=3/4 |
| Secante | H/CA=5/4 | H/CA=5/3 |
| Cosecante | H/CO=5/3 | H/CO=5/4 |
Vea también Teorema de Pitágoras.
Funciones trigonométricas en el círculo trigonométrico
El círculo trigonométrico es aquel cuyo radio vale la unidad. Al trazar dos ejes perpendiculares entre sí que pasan por el origen del círculo, tendremos un sistema de ejes coordenados XY. Para calcular las diferentes funciones trigonométricas, nos valdremos de estos ejes.
Función trigonométrica seno
En un ángulo interno en el círculo trigonométrico cuyos segmentos son igual al radio 1, el seno será la proyección del segmento móvil sobre el eje de las ordenadas Y. Imaginemos una linterna iluminando este segmento móvil dentro del círculo. La sombra que proyecta el segmento sobre el eje Y será el valor del seno.
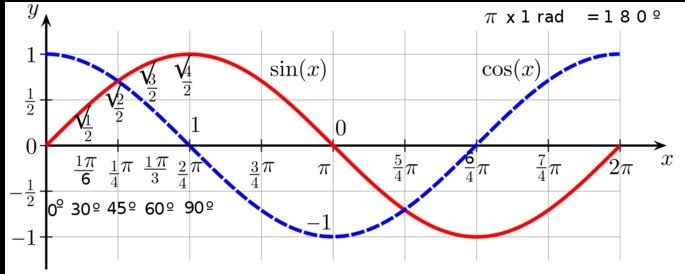
Cuando se grafica el seno a medida que el segmento se abre, el seno crece hasta ser igual a 1, cuando el ángulo es igual a 90º o 1/2π. Desde los 90º a los 180º el seno se reduce, pero sigue siendo positivo. Por encima de los 180º el seno toma valores negativos hasta llegar a los 360º. Los valores del seno se hallan entre 1 y -1.
Función trigonométrica coseno
En un ángulo interno en el círculo trigonométrico cuyos segmentos son igual al radio 1, el coseno será la proyección del segmento móvil sobre el eje de las abscisas X. Imaginemos una linterna iluminando este segmento móvil dentro del círculo. La sombra que proyecta el segmento sobre el eje X será el valor del coseno.
Cuando se grafica el coseno a medida que el segmento se abre, el coseno se reduce hasta ser igual a 0 cuando el ángulo es igual a 90º o 1/2π. Desde los 90º a los 270º el coseno toma valores negativos. Por encima de los 270º el coseno vuelve a tomar valores positivos hasta llegar a 1 en los 360º. Los valores del coseno se hallan entre 1 y -1.
Función trigonométrica tangente
En un ángulo interno en el círculo trigonométrico cuyos segmentos son igual al radio 1, la tangente será la extensión del segmento móvil sobre el eje de las ordenadas Y. Imaginemos una pared pegada del círculo y el segmento móvil se estira hasta tocar la pared. La distancia desde la base de la pared hasta donde el segmento toca la misma será el valor de la tangente.
Cuando se grafica la tangente a medida que el segmento se abre, esta crece hasta valores en el infinito ∞ cuando el ángulo es igual a 90º o 1/2π. Desde los 90º a los 180º toma valores negativos. Por encima de los 180º la tangente vuelve a tomar valores positivos hasta 270º. A partir de 270º vuelve a tomar valores negativos hasta llegar a 0 en los 360º. Los valores de la tangente se hallan entre ∞ y -∞.
Funciones trigonométricas recíprocas
Si, por ejemplo, una razón es a/b, entonces, el recíproco es b/a, de esta manera, las funciones trigonométricas poseen funciones recíprocas en el mismo ángulo. Estas son:
| Función trigonométrica | Función recíproca |
|---|---|
| Seno | Cosecante |
| Coseno | Secante |
| Tangente | Cotangente |
Características de las funciones trigonométricas
Cuando vemos un gráfico de una función donde se repiten las formas decimos que son periódicas. Las funciones trigonométricas son periódicas. La periodicidad puede verse en un electrocardiograma.
"Las funciones trigonométricas de un ángulo son iguales, en valor absoluto y en signo, a las cofunciones del ángulo complementario por defecto."
Por ejemplo:
Observa que 60° y 30° son ángulos complementarios, y seno y coseno son cofunciones.
En este caso, 70° y 20° son ángulos complementarios, y tangente y cotangente son cofunciones.
"Las funciones trigonométricas de un ángulo son iguales en valor absoluto a las funciones del ángulo complementario ( osea que suma 360°), pero de signo contrario excepto el coseno y la secante que son del mismo signo".
Por ejemplo:
"Las funciones trigonométricas de un ángulo son iguales en valor absoluto a las funciones trigonométricas del ángulo suplementario (es decir, el que suma 180°), por defecto, pero de signo contrario, con excepción del seno y de la cosecante que son del mismo signo".
Por ejemplo:
Resumen de los valores de las funciones trigonométricas de ángulos notables
| Ángulo | Seno | Coseno | Tangente |
|---|---|---|---|
| 0º | 0 | 1 | 0 |
| 30º |  |
 |
 |
| 45º |  |
|
1 |
| 60º | |
|
 |
| 90º | 1 | 0 |  |
| 180º | 0 | -1 | 0 |
| 270º | -1 | 0 |  |
Ejemplos de funciones trigonométricas
En la naturaleza encontramos diferentes manifestaciones que pueden ser analizados por medio de funciones trigonométricas.
Horas de luminosidad en las zonas templadas
Entre el trópico de Cáncer y el círculo polar ártico en el hemisferio norte, y el trópico de Capricornio y el círculo polar antártico en el hemisferio sur, encontramos un patrón de iluminación solar característico. Esto lo vemos reflejado en las estaciones, con menor cantidad de luz solar en invierno y mayor cantidad de luz en los meses de verano.
Este patrón de iluminación natural sigue una función sinusoidal a lo largo del año.
Vea también:
- Problemas y ejercicios de funciones trigonométricas (resueltos)
- Ángulos: qué son, tipos y ejemplos
- Qué son las Matemáticas
- Qué es una Función
