Las fracciones son la representación de las partes de un todo. Cuando dividimos algo en partes iguales y tomamos una cierta cantidad de estas, la forma de mostrarlo es a través de fracciones. Lo que estamos dividiendo es un entero y cada parte es una fracción de ese entero.
Partes de una fracción
En las fracciones, el número que va arriba (término superior) es el numerador, que son las partes que se ha tomado de un todo. El número que va abajo es el total de partes en que se dividió el entero y se llama denominador.
Si cortamos una pizza en 8 partes iguales, cada tajada es un octavo (1/8 ) del total. Si te comes tres tajadas, puedes decir que comiste tres octavos (3/8) de la pizza. En este caso, el denominador siempre será 8.

Tipos de fracciones
Fracción propia
Son fracciones en que el numerador es menor que el denominador, es decir, representa un número menor que un entero. Un quinto, cinco octavos y veinticinco ochentaiochoavos son ejemplos de fracciones propias:
Fracción impropia
Son fracciones en que el numerador es mayor que el denominador, es decir, representa un número mayor que el entero. Por ejemplo, ocho quintos, tres medios y quince décimos:
Fracción aparente
Son fracciones en que el numerador es múltiplo del denominador, es decir, representa un número entero escrito en forma de fracción. Por ejemplo, ocho cuartos, que vendría a ser igual a dos:
Fracción mixta
La fracción mixta combina partes enteras con fracciones propias. Es lo mismo que decir que tenemos más de una cosa dividida en la misma cantidad de porciones. Por ejemplo, tienes dos sandias y cada una la picas en seis, pero solo se comen ocho pedazos, lo cual vendría a ser un entero y dos sextos:
Fracciones comunes y decimales
Fracciones comunes son aquellas cuyo denominador no es la unidad seguida de ceros. Por ejemplo, un tercio, dos séptimos, nueve onceavos:
Las fracciones decimales son aquellas cuyo denominador es la unidad seguida de ceros. Como, por ejemplo, tres décimos, veinticinco centésimas y una milésima:
Operaciones con fracciones
Adición de fracciones con igual denominador
En la adición o suma de fracciones, cuando los denominadores son iguales, se suman los numeradores y se deja igual el denominador. Por ejemplo:
Adición de fracciones con diferente denominador
Cuando los denominadores son diferentes, transformamos las fracciones para que tengan el mismo denominador. Para esto, se utiliza el mínimo común múltiplo (mcm) de los denominadores, es decir el número más pequeño múltiplo de los denominadores. Luego, el mcm se divide por cada denominador y el resultado multiplica a su numerador correspondiente. Por ejemplo:
Los denominadores son 5 y 4, por lo tanto, el mcm es 20. Se divide 20 entre 5 y el resultado multiplica el numerador 1. De esta manera, 20 ÷ 5 = 4. Por su parte, 4 × 1 = 4. La fracción, de este modo, se transformará en:
Por otro lado, se divide 20 entre 4 y el resultado multiplica al numerador 3. Así, pues, 20 ÷ 4 = 5. Por otra parte, 5 × 3 = 15. De esta forma, la fracción se transformará en:
Ahora, las dos fracciones tienen el mismo denominador (20) y se facilita la suma de los numeradores (4 y 15):
Vea también Suma de fracciones.
Sustracción o resta de fracciones con igual denominador
En la sustracción o resta de fracciones, cuando los denominadores son iguales, se restan los numeradores y se deja igual el denominador, por ejemplo:
Sustracción de fracciones con diferente denominador
Cuando los denominadores son diferentes, transformamos las fracciones para que tengan el mismo denominador. Para esto se utiliza el mínimo común múltiplo (mcm) de los denominadores, es decir, el menor número múltiplo de los denominadores. Luego, el mcm se divide por cada denominador y el resultado multiplica a su numerador correspondiente. Por ejemplo:
Los denominadores son 3 y 4, por lo tanto, el mcm sería 12. Dividimos 12 entre 3, y el resultado multiplica el numerador 2. Así, pues, 12 ÷ 3 = 4, y, a su vez, 4 × 2 = 8. De este modo, la fracción se transforma en:
A continuación, 12 divide al 4 y el resultado multiplica al numerador 2. De esta manera, 12 ÷ 4 = 3, esto sería: 3 × 2 = 6. De modo que la fracción se transforma en:
Ahora que ambas fracciones tienen el mismo denominador podemos restar fácilmente:
Vea también Suma y resta de fracciones.
Multiplicación de fracciones
En la multiplicación de fracciones, se multiplican los numeradores entre sí y los denominadores entre sí. Como en el ejemplo a continuación:
División de fracciones
Cuando queremos dividir dos fracciones, dejamos la primera fracción igual, invertimos el numerador y el denominador de la segunda fracción y luego se multiplican entre si las fracciones, así:
Vea también:
Problemas de fracciones (resueltos)
1. ¿Cómo se llaman las partes iguales en que se divide la unidad si se divide en 10, 12, 15, y 27 partes?
2. ¿Cuántos tercios hay en una unidad, en dos unidades, en tres unidades?
3. Si una naranja se divide en cinco partes, y a una persona se le dan tres pedazos y a otra el resto, ¿Cómo se llaman las partes que se le ha dado a cada uno?
4. Escriba las fracciones: siete décimos, catorce diecinueveavos, y treinta ciento treintaidosavos.
5. De las siguientes fracciones, ¿cuáles son propias?
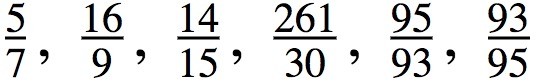
6. Una persona vende 1/8 de su finca, alquila 1/8, y el restante lo cultiva. ¿Qué porción de la finca cultiva?
7. El kilo de limones cuesta 3/4 $ ¿Cuánto cuestan 8 kilos?
8. En un colegio hay 324 alumnos y el número de alumnas es 7/18 del total. ¿Cuántos varones hay?
9. Dividir 2/5 ÷ 7/10.
10. 11/14 ÷ 7/22.
11. La distancia entre dos ciudades es de 140 km. ¿Cuántas horas debe caminar una persona que recorre 3/14 de dicha distancia en una hora para ir de una ciudad a otra?
Vea también Problemas de fracciones
(Texto traducido y adaptado por Ana Zita).