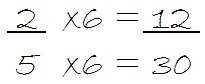Las fracciones equivalentes son fracciones que no tienen el mismo numerador y denominador pero que representan la misma cantidad. Por ejemplo, las fracciones ,
o
, todas representan la misma cantidad que es la mitad de una unidad, como puedes ver en el siguiente dibujo.

También puedes verificar en la ilustración que sigue, que las fracciones y
son equivalentes porque representan la misma cantidad.

Las fracciones equivalentes se usan para hacer operaciones como la suma y la resta, puesto que para poder llevar a cabo esas operaciones es necesario que todas las fracciones involucradas tengan el mismo denominador.
Cómo sacar fracciones equivalentes
Supongamos que tienes una fracción, por ejemplo , y que quieres obtener una fracción equivalente. Para encontrarla puedes seguir uno de los dos métodos que te presentamos a continuación.
Por amplificación
Para esto tienes que multiplicar tanto el numerador como el denominador, por un mismo número que tú puedes elegir. Por ejemplo, escojamos el 3, entonces multiplicas el numerador y el denominador por 3, de la siguiente manera.
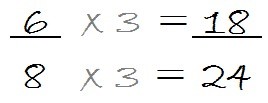
De esta forma la fracción que obtuvimos es equivalente a
.
Con este método, simplemente cambiando el número por el cual vas a multiplicar, puedes generar tantas fracciones equivalentes como quieras. Ahora generemos 4 fracciones equivalentes a , multiplicando por 2, 3, 4 y 5.
|
Fracción original |
Número por el que se multiplica | Fracción equivalente |
|---|---|---|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
Por simplificación
El segundo método consiste en dividir ambos números: el numerador y el denominador por un mismo número. En este caso, no podemos usar cualquier número, sino que debes elegir un divisor de los dos números que forman la fracción.
En nuestro ejemplo, donde buscamos fracciones equivalentes para , podemos usar el 2 porque sí divide a 6 y a 8, pero no podríamos usar el 5 porque 5 no divide a 6 ni a 8. Lo hacemos de la siguiente manera.
Así, la fracción que obtuvimos dividiendo es equivalente a
Ver también Operaciones con fracciones
Cómo saber si dos fracciones son equivalentes
Para poder determinar si dos fracciones denotan la misma cantidad, o sea si son equivalentes, se usa el método conocido como productos cruzados.
Este método consiste en comparar el resultado de dos multiplicaciones que debes efectuar. La primera multiplicación será el numerador de la primera fracción por el denominador de la segunda fracción, la segunda multiplicación es el denominador de la primera por el numerador de la segunda. Si el resultado de ambas multiplicaciones es el mismo, entonces las fracciones son equivalentes.
Por ejemplo, determinemos si es equivalente a
. Para esto, haremos las multiplicaciones mencionadas.

Como los resultados de las multiplicaciones no son los mismos, las fracciones no son equivalentes.
Productos cruzados: explicación paso a paso
Recuerda que las fracciones solo se pueden comparar si ambas tienen el mismo denominador, por lo que si las fracciones tienen distinto denominador, tendremos que convertirlas. En otras palabras, tenemos que encontrar fracciones equivalentes a las que queremos comparar, y estas deben tener el mismo denominador.
Para convertir las fracciones utilizamos el método de amplificación que explicamos antes, es decir, vamos a multiplicar numerador y denominador de cada una por un determinado número.
La elección del número con el que vamos a multiplicar cada fracción es la clave para lograr que las fracciones que obtengamos tengan los mismos denominadores, y así, podamos compararlas.
Veamos un ejemplo, determinemos si son equivalentes las fracciones y
.
Paso 1) Tomamos la primera fracción y multiplicamos numerador y denominador por 4, que es el denominador de la segunda fracción.
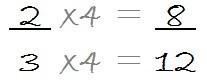
De esta manera obtenemos , que es una fracción equivalente a
.
Paso 2) Tomamos la segunda fracción y la multiplicamos por 3, que es el denominador de la primera fracción.
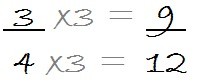
La fracción que obtuvimos es equivalente a
.
Paso 3) Comparamos las fracciones que obtuvimos. Como y
no denotan la misma cantidad, no son fracciones equivalentes, y tampoco lo son las fracciones originales
y
.
Vea también:
Ejercicios (con respuestas):
1) Determina si las fracciones y
son equivalentes.
2) Determina si las fracciones y
son equivalentes.
3) Encuentra una fracción equivalente a cuyo denominador sea
.